1. Introduction

K-Nearest Neighbour is one of the simplest Machine Learning algorithms based on Supervised Learning technique. K-NN algorithm assumes the similarity between the new case/data and available cases and put the new case into the category that is most similar to the available categories. K-NN algorithm stores all the available data and classifies a new data point based on the similarity. This means when new data appears then it can be easily classified into a well suite category by using K- NN algorithm. K-NN algorithm can be used for Regression as well as for Classification but mostly it is used for the Classification problems. K-NN is a non-parametric algorithm, which means it does not make any assumption on underlying data. It is also called a lazy learner algorithm because it does not learn from the training set immediately instead it stores the dataset and at the time of classification, it performs an action on the dataset.

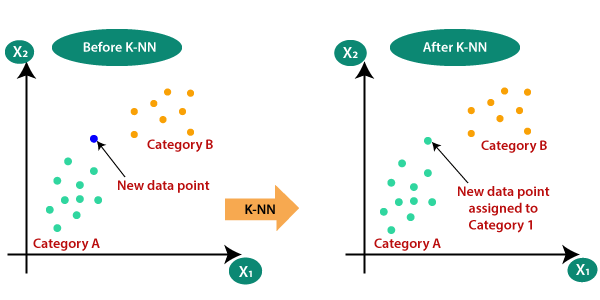
Suppose there are two categories, i.e., Category A and Category B, and we have a new data point x1, so this data point will lie in which of these categories. To solve this type of problem, we need a K-NN algorithm. With the help of K-NN, we can easily identify the category or class of a particular dataset. Consider the below diagram:

The K-NN working can be explained on the basis of the below algorithm:
Step-1: Select the number K of the neighbors.
Step-2: Calculate the Euclidean distance of K number of neighbors.
Step-3: Take the K nearest neighbors as per the calculated Euclidean distance.
Step-4: Among these k neighbors, count the number of the data points in each category.
Step-5: Assign the new data points to that category for which the number of the neighbor is maximum.
Step-6: Our model is ready.

Suppose we have a new data point and we need to put it in the required category. Consider the below image:

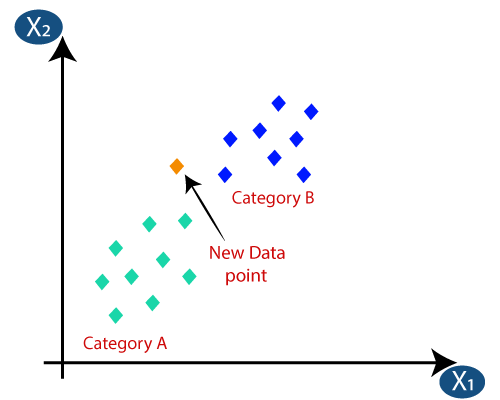
Firstly, we will choose the number of neighbors, so we will choose the k=5. Next, we will calculate the Euclidean distance between the data points. The Euclidean distance is the distance between two points, which we have already studied in geometry. It can be calculated as:

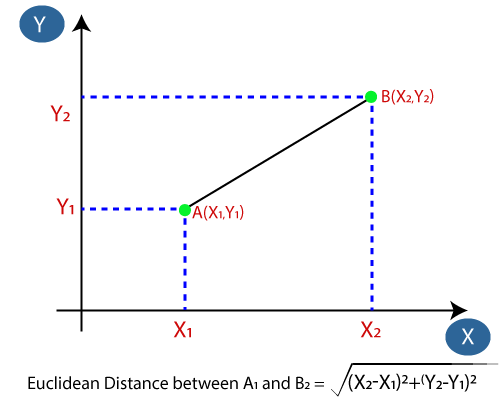
By calculating the Euclidean distance we got the nearest neighbors, as three nearest neighbors in category A and two nearest neighbors in category B. Consider the below image:

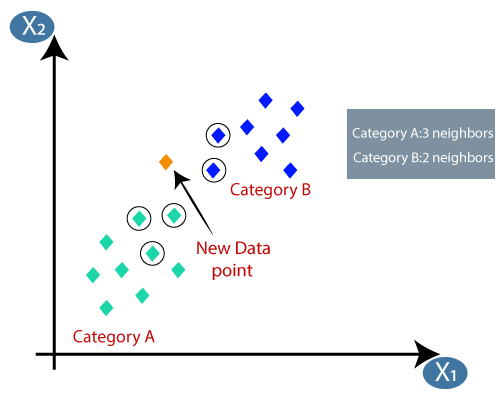
As we can see the 3 nearest neighbors are from category A, hence this new data point must belong to category A.

2. Codes

Input

import numpy as np

def euclidean_distance(x1, x2):

"""

Calculates the Euclidean distance between two vectors.

Args:

x1: A numpy array of the first vector.

x2: A numpy array of the second vector.

Returns:

The Euclidean distance between the two vectors.

"""

return np.sqrt(np.sum((x1 - x2)**2))

def knn(x_train, y_train, x_test, k):

"""

Performs k-nearest neighbors classification on a test set.

Args:

x_train: A numpy array of the training data features.

y_train: A numpy array of the training data labels.

x_test: A numpy array of the test data features.

k: The number of neighbors to use for classification.

Returns:

A numpy array of the predicted labels for the test data.

"""

# Calculate the distances between the test data and the training data.

distances = np.array([euclidean_distance(x_test, x_train) for x_train in x_train])

# Find the indices of the k nearest neighbors for each test data point.

nearest_neighbors = np.argsort(distances)[:, :k]

# Predict the labels for the test data points using the labels of the k nearest neighbors.

predicted_labels = np.array([y_train[i] for i in nearest_neighbors])

return predicted_labels

[5, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1]

3. Distance Metrics Used in KNN Algorithm

As we know that the KNN algorithm helps us identify the nearest points or the groups for a query point. But to determine the closest groups or the nearest points for a query point we need some metric. For this purpose, we use below distance metrics:

• Euclidean Distance - This is nothing but the cartesian distance between the two points which are in the plane/hyperplane. Euclidean distance can also be visualized as the length of the straight line that joins the two points which are into consideration. This metric helps us calculate the net displacement done between the two states of an object.
  
  
• Manhattan Distance - This distance metric is generally used when we are interested in the total distance traveled by the object instead of the displacement. This metric is calculated by summing the absolute difference between the coordinates of the points in n-dimensions.
  
  
• Minkowski Distance - The Minkowski distance or Minkowski metric is a metric in a normed vector space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance. It is named after the German mathematician Hermann Minkowski.

4. How to choose the value of k for KNN Algorithm?

The value of k is very crucial in the KNN algorithm to define the number of neighbors in the algorithm. The value of k in the k-nearest neighbors (k-NN) algorithm should be chosen based on the input data. If the input data has more outliers or noise, a higher value of k would be better. It is recommended to choose an odd value for k to avoid ties in classification. Cross-validation methods can help in selecting the best k value for the given dataset.

5. Applications of the KNN Algorithm

• Data Preprocessing While dealing with any Machine Learning problem we first perform the EDA part in which if we find that the data contains missing values then there are multiple imputation methods are available as well. One of such method is KNN Imputer which is quite effective ad generally used for sophisticated imputation methodologies.
  
  

• Pattern Recognition KNN algorithms work very well if you have trained a KNN algorithm using the MNIST dataset and then performed the evaluation process then you must have come across the fact that the accuracy is too high.
  
  

• Recommendation Engines The main task which is performed by a KNN algorithm is to assign a new query point to a pre-existed group that has been created using a huge corpus of datasets. This is exactly what is required in the recommender systems to assign each user to a particular group and then provide them recommendations based on that group s preferences.

6. Advantages of the KNN Algorithm

• Easy to implement as the complexity of the algorithm is not that high.
  
  

• Adapts Easily As per the working of the KNN algorithm it stores all the data in memory storage and hence whenever a new example or data point is added then the algorithm adjusts itself as per that new example and has its contribution to the future predictions as well.
  
  

• Few Hyperparameters The only parameters which are required in the training of a KNN algorithm are the value of k and the choice of the distance metric which we would like to choose from our evaluation metric.

• Does not scale As we have heard about this that the KNN algorithm is also considered a Lazy Algorithm. The main significance of this term is that this takes lots of computing power as well as data storage. This makes this algorithm both time-consuming and resource exhausting.
  
  

• Curse of Dimensionality There is a term known as the peaking phenomenon according to this the KNN algorithm is affected by the curse of dimensionality which implies the algorithm faces a hard time classifying the data points properly when the dimensionality is too high.
  
  

• Prone to Overfitting As the algorithm is affected due to the curse of dimensionality it is prone to the problem of overfitting as well. Hence generally feature selection as well as dimensionality reduction techniques are applied to deal with this problem.